Firstly, in order to test linear regression assumptions in baseball I need to choose the best linear regression model I’ve created so far. The best model created thus-far is Wins=BAx+RBIy+HRz. This means that team wins can be predicted by batting average, runs batted in, and home runs. Now I will first test assumption 2, making sure that there is no perfect multicollinearity.

Using the cor(cbind()) formula you see that there is no -1 or 1 correlation meaning that no perfectly multicollinearity exits. However, the data is above 0 which means the variables are not independent. Now onto assumption 3 which tests to see whether errors are independent. First, I ran my standard model using fit=lm(). Then I used fit$resid[1:5] to show how far off from the line my variables are. Next, I created a scatter plot to visualize the data. This was then followed by testing for autocorrelation, which is the correlation of a variable with itself.

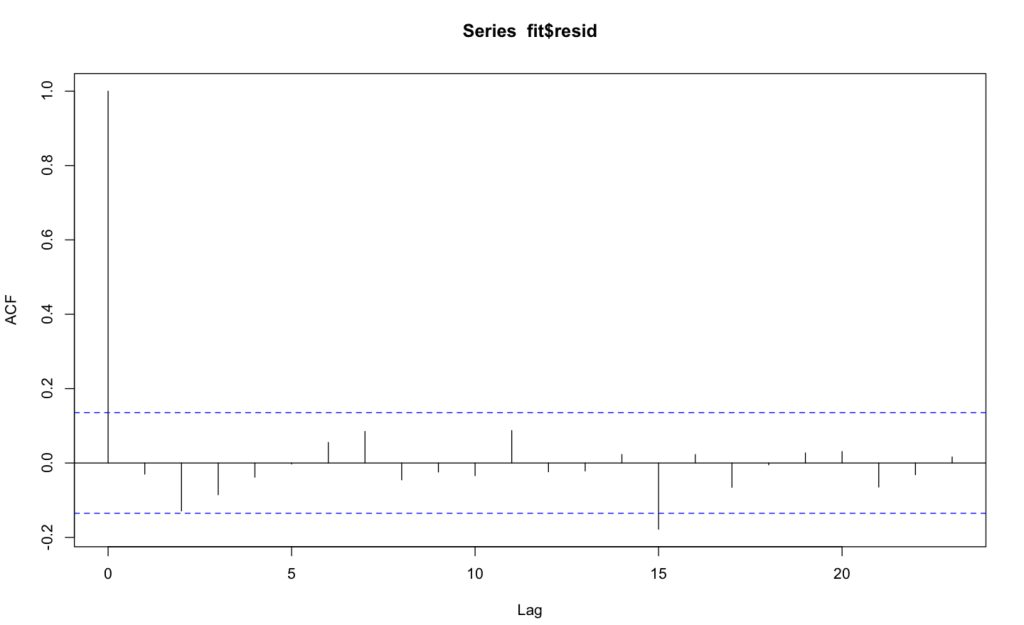
As you can see, the bar at lag 15 goes outside the blue dotted line meaning the data is significant. For the fourth assumption, the data is going to be tested to make sure there is no heteroskedasticity. This basically means that a model is better at predicting certain variables over others.
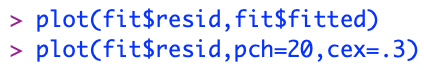
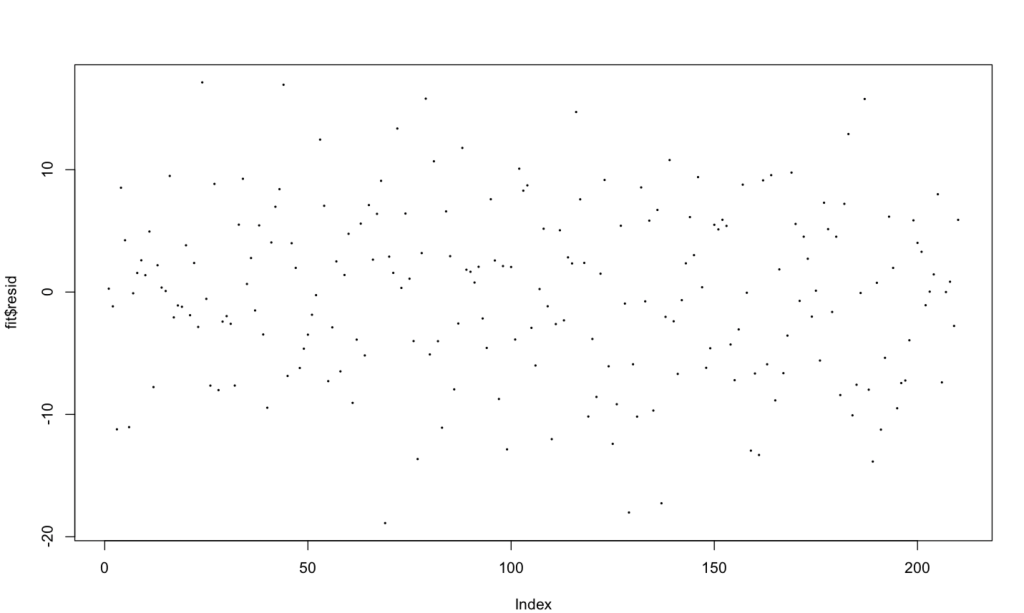
In the plot above there is no general pattern which means there is no heteroskedasticity. Finally, for assumption 5 the data will be tested to make sure the errors are normally distributed. First, I created a histogram showing wins and plotted percentiles of response (Y) against the percentiles of the normal distribution (X). Then using qqline() I plotted the line across the percentiles.

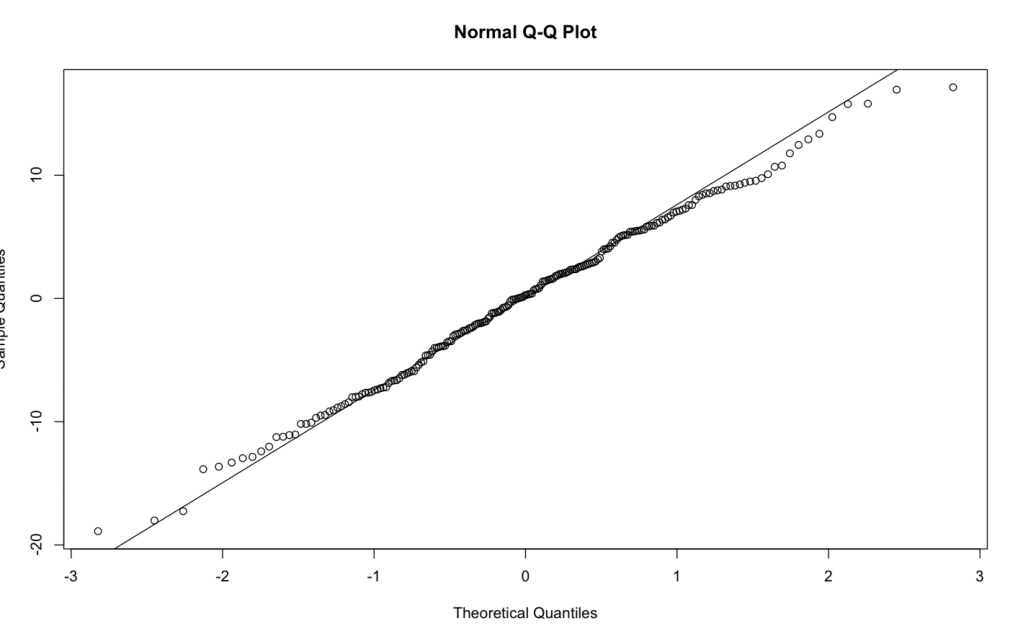
Because there is a straight line it means the distributions are equal (normal)
