To test the assumptions and requirements of logistic regression models, I will use the same model as used in the last post.
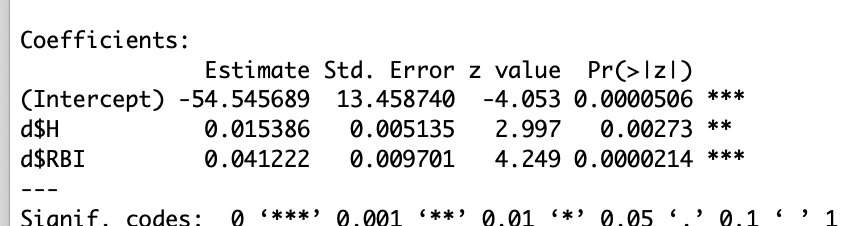
I will test the assumptions and requirements the same as we used for the linear regression models. The logistic regression model is log(p/(1-p))=-54.54+.015*Hits+.04*RBI, where the intercept is the binary variable of “fivehundred”. First I will test assumption two, making sure there is no perfect multicollinearity.

Using the cor(cbind()) formula you can see that there is no 1 to 1 correlation between variables meaning that no perfect multicollinearity exists. Now to see whether my errors are independent I used the standard fit=glm() logistic regression model. Then I used fit$resid[1:5] to show how far off from the line my variables are. This was then followed by testing for autocorrelation.

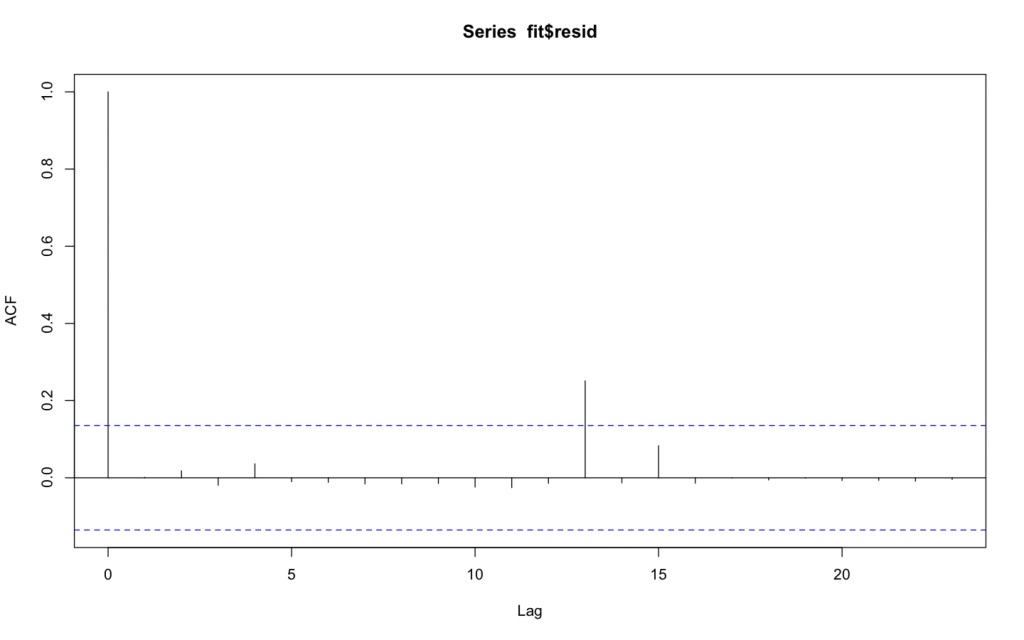
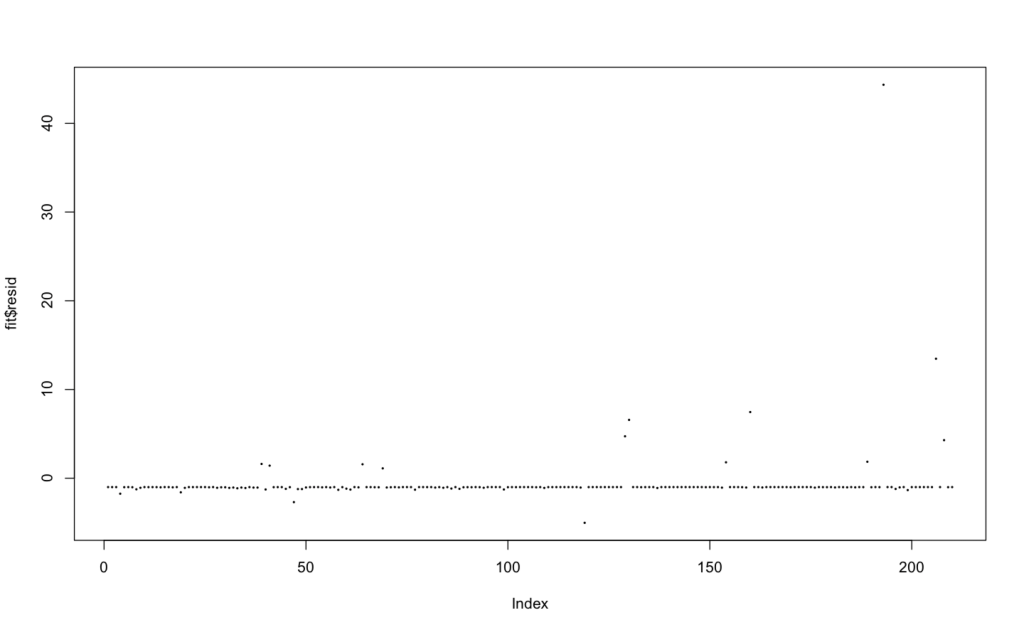
As you can see, at lag 13 the line eclipses the blue dotted line meaning the data is significant. For the fourth assumption, the data is going to be tested to make sure there is no heteroskedasticity. When the plot is run I found that there was a general straight line with a couple outliers as the index increases. However, variance is increasing as X increases meaning there is no heteroskedasticity.
Now for the fifth assumption the data will be tested to make sure the errors are normally distributed. To do this I will plot a histogram and qqline of the binary variable in R.

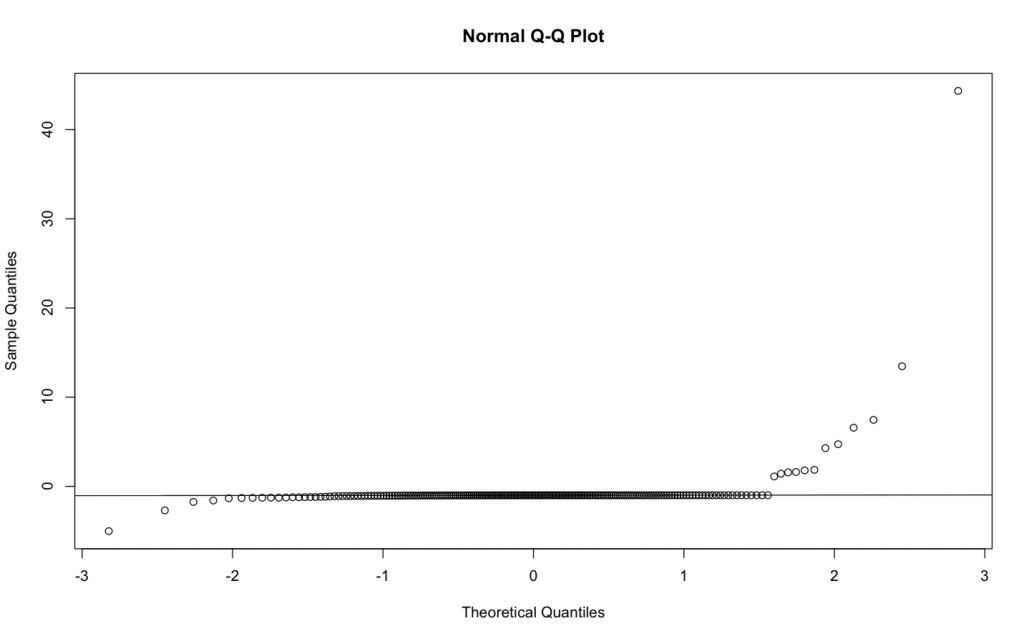
Because there is a straight line it means that the distributions are normal (equal). Now a specific requirement for logistic regression is the test to make sure there is no complete separation. Complete separation occurs when one or more variables classifies the observations into success and failure perfectly. To do this I plotted hits and RBI’s against my binary variable “fivehundred” (teams hitting above .270).

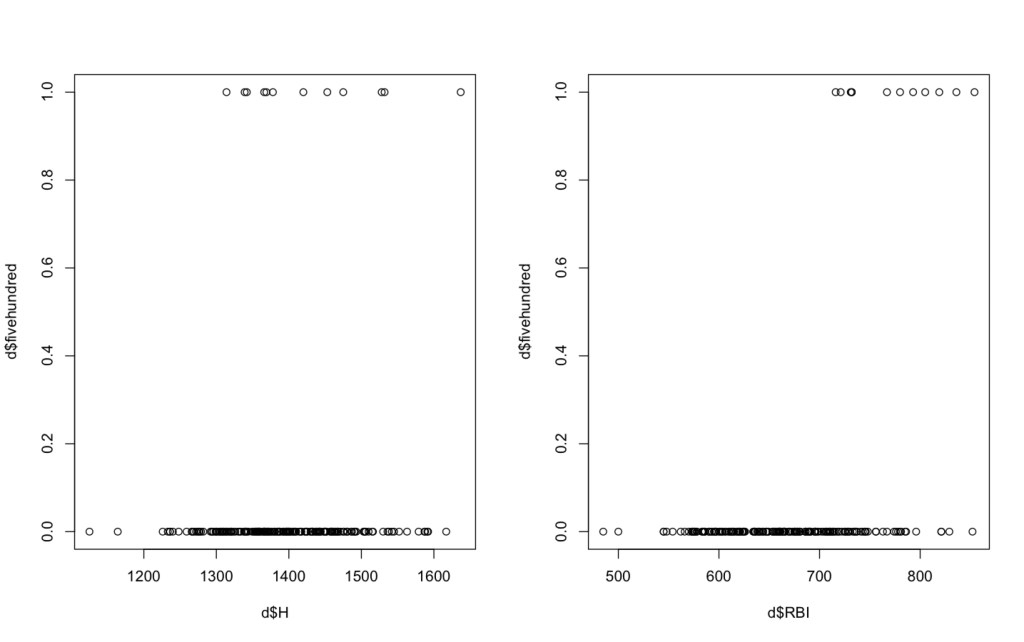
Because no vertical line can be drawn in either plot to separate teams that had a batting average over .270 by hits and RBI’s, this model is not suffering from complete separation. Finally, the last requirement is having a large sample size. The MLB data from 6 seasons only has 2010 observations. Because it doesn’t have thousands of observations, my model does not pass the large sample requirement.
