In order to build a model that accurately can predict the amount of wins an MLB team will get, we want to be able to use all the predictor variables. Then we can study the importance of each variable using backward stepwise selection. To do this, I utilized a linear regression model because it gives us an R-squared variable. This R-squared variable is essential to seeing the accuracy of the model and its predictors.
In my linear regression model, as previously stated, I will be using team wins as my response variable. I then dived my data into training and test sets to randomly assign 70% of the data.

My data set has 29 variables, so I will use wins as my response variable (variable I am trying to predict) and the other 28 as predictors (X variables).

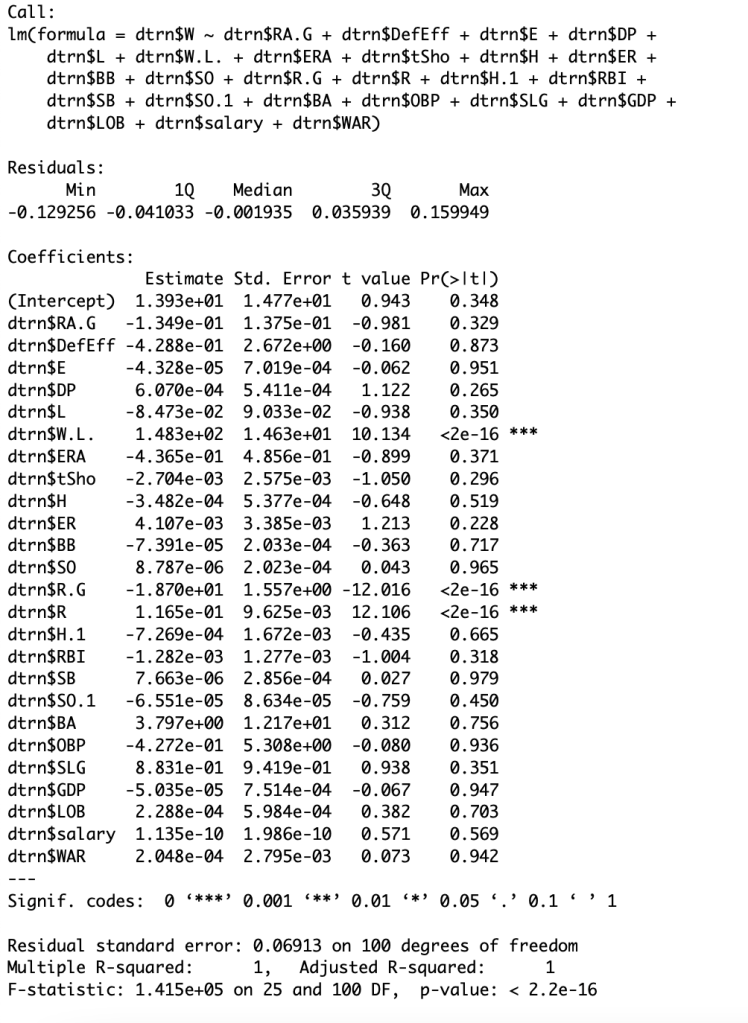
As you can see, only three variables are considered significant. Those are W.L. ,R.G, and runs scored. To explain, W.L. is a teams win loss percent when it comes to pitching. When a starting pitcher has a substantial enough lead when pulled out of the game, he gets the win. However, if a starting pitcher gives up enough runs to cost their team the game they get the loss. This W.L. statistic puts that data into a win percentage per team. R.G is the runs scored per game average for a team and R is total runs over the season. Now down bellow is my new model using only significant predictors.
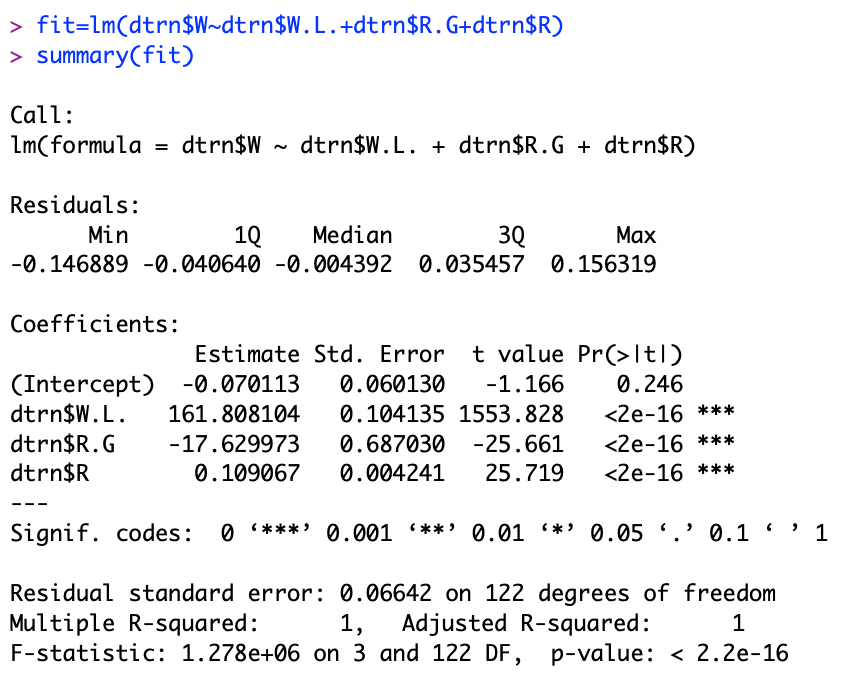
The R-squared variable is still a 1 with fever variables, meaning that the regression prediction perfectly fits the data. This means that W.L. percent, R.G percent, and runs scored account for 100% of the variability in the data. Now I will do backwards stepwise selection to see what variables are contributing the least in this new regression equation.

First I removed W.L. percentage, which resulted in an R-squared drop from 1 to .37. This means that W.L. is contributing 63% of the R-squared.
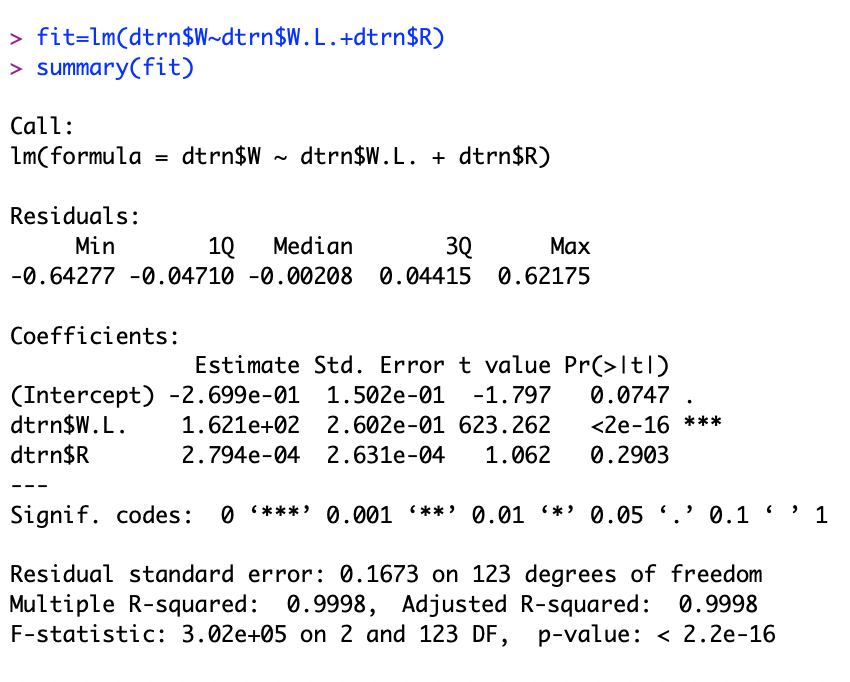
When R.G is removed and replaced with W.L. , R-squared rises to almost 100%. This means that R.G contributes almost nothing.

Finally, when R (runs) is scored R-squared remains at almost 100%. Like R.G, runs contributes almost nothing to the model.
After removing each variable it loos like W.L. percentages contributes the most to the model at 63%. Because two of the contributors weren’t helpful in the model (didn’t contribute much to R-sqaured) they need to be removed. However, because no other variables are significant, I cannot replace the variables that got removed. Therefore, it looks like (for now) that W.L. percent is the largest predictor of team wins.
